What do games using loot drops and games using AI driven by behavioural parameters such as sleep, hunger and happiness have in common? At first glance, not much. But it is very likely that both of them deploy the same algorithm. Let’s start by example:

There’s plenty of games using loot drops today. It’s an easy way to implement a form of replayability in a game, where character progression is tied to the gear they are wearing. By not guaranteeing you’ll get what you want in your first content playthrough, the likelihood is that you will have to play it more than once to achieve what you wanted.

On the other hand there’s the AI with the internal parameters. The most common example is the Sims, as one of the game’s core loops is making sure your character does not end up in the red and executes undesirable behaviours like pooping on the floor or lighting the kitchen on fire. Or maybe your aim is to turn your Sims house and its inhabitants into a flaming hellhole with no doors (or even more terrifying, swimming pools without ladders) – I won’t judge.

Either way, what both of the Sims AI and the loot drops have in common, is that the game is allowed to make decisions about what happens. And to avoid being predictable, these decisions are randomized. In the case of the loot dropping, the game is asked “what will you give to the player?” which then generates one or more items. In the Sims scenario, the AI is similarly asked “what do you want to do now?” and once again, the outcome is randomized. Each time it is an assortment of options, weighed against each other – which is where the term “weight-based” randomization comes from.

In both of these cases, having the outcome be 100% random is not desirable. Instead you want the likelihood of certain outcomes to be higher than the others: You want rarer loot to drop less often, or the Sims to execute behaviours related to their more critical internal states than those better off (no time for TV if they REALLY have to go potty-time).

Hell, you can even use the same algorithm for targeted advertisement on your website or application – favouring some advertisements above others, but not completely outruling those of less relevance (who knows, the user may respond well to what you thought was irrelevant and then you can favor those a little higher). It would be easy to balance the weights to favor the themes the user responds to, showing more of that.

Which finally brings me to the point – what does the algorithm look like and how can you implement it in your own work? Let’s do some math.

The algorithm

Before we get knee deep into the numbers, let’s first discuss some terminology, so that you may explain your sudden stroke of genius to your peers with the correct words.

The Terminology:

For starters, picking an outcome based on a “value” it has been given, is commonly referred to as “selection by utility value.” A higher value is more desirable. The value itself can be assigned directly or generated by the game – it depends on the context. For example loot drop rates is a constant number – set by the game designer, whereas the Sims internal values are constantly changing.

Absolute utility:

Absolute utility is quite simple. All options are evaluated and the one with the highest utility value is chosen. If two or more options have exactly the same utility value, it is common to randomly choose between them (or whatever is deemed the most optimal for your context). The downside of absolute utility is how predictable it becomes, and can be exploited by players who figure out how it assigns its values, to force a certain outcome.

Relative utility:

Relative utility also uses utility values, but does not blindly select the one with the highest value. Instead, the utility values are used to determine the likelihood of the outcome being chosen – favoring the outcomes with the higher values, but never guaranteeing anything. This is what we want.

Isn’t it lovely how the same process is called “weight-based random,” depending on who you ask? Let’s be honest, while relative utility sounds more elegant, it doesn’t really ring “self-explanatory terminology!” Because of this, I will continue to refer to this process as weight-based randomization, as it describes the process better. If there’s an easier word for something complicated, never shy away from using it. But of course, if you’re talking to your maths professor, it might be a different story.

The Equation:

There’s a few steps involved in arriving at an outcome, but at the heart of it all sits a fairly simple equation. Or, well, aside from the epsilon symbol:

To understand what we’re looking at here, understand that there are a few steps which must be taken, to get to where we want and select an outcome. What this equation shows is the first step. The “utility value (U)” for an outcome is converted to a “probability value (P).”

The equation above works on the following assumptions:

• The utility values of all outcomes are stored in the array U[ ].
• The calculated probability values will be stored in the array P[ ].
• An outcome is identified by having the same index number in both P and U – eg. U[0]’s probability value is stored in P[0].

Workin by these assumptions, we can calculate P[0] by:

• P[0] = U[0] / The sum of all other utility values

But if we’re working through all of the utility values, it becomes a little harder to illustrate with the epsilon symbol, as we’d have to skip the index we’re working from. But computationally, it’s easy:

• P[i] = U[i] / (The sum of all utility values – U[i])

That’s it! No more hocus pocus. To explain the epsilon symbol, it simply means the sum of an array of numbers. Which is great if you’re only calculating P[0], but once you go to P[1] and up, you need a more complex expression. You really don’t have to be able to write it like this, but I think it’s a fun exercise:

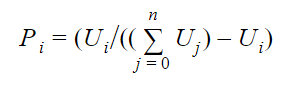
The recipe:

Once all of the probability values have been calculated and stored in the P array, we can perform the next steps and find an outcome:

1. Add the sum total of all probability values in P
2. Pick a random number between zero and this total sum
3. Going through each index in P, subtract the probability value in that index, from the total sum. Keep moving to the next index and doing the same, until the total sum is zero or less.
4. The index which caused this final subtraction, is the index of the outcome chosen (eg. the outcome whose utility value was stored at that index in U originally).

Let me illustrate with an example. Consider the following utility values:

U₀ = 3

U₁ = 5

U₂ = 7

U₃ = 8

I’ve then calculated the probability for each of these options:

P₀ = 0.15

P₁ = 0.278

P₂ = 0.438

P₃ = 0.53

Adding these numbers together I get:

Sum of weights = 1.396

Now I’ll take a random number between zero and the sum of the probability values. For the sake of demonstration we’ve simply picked 0.9. The selection process then looks like this:

P₀) 0.9 – 0.15 = 0.75

P₁) 0.75 – 0.278 = 0.472

P₂) 0.472 – 0.438 = 0.034

P₃) 0.034 – 0.53 = -0.496 ←- This option is chosen

Remember to stop the process at or below zero. If I had gotten a random number just a little lower than 0.9 I would likely have landed on the third option instead of the last one; just look at how close P₂ comes to zeroing out.

The prototype:

Oh no. You knew I had to do it. Just writing about theory is not good enough for me! I created a prototype to illustrate how the system works in practice. In this prototype, you must press play to generate a list of utility values. You can then configure your own utility values for each of the options, then press “space” to let the algorithm run however many times you’ve specified, and have the result be visualized on the screen. The taller a block is, the more times that outcome was chosen.

Going this far, I’ve almost outlined the pseudocode by describing the algorithm. Because of this, I will simply write the code documentation and let the resultspeak for itself:

• Download the Unity Package file

But before we get to the code, here’s a quick how-to on how to run the project:

1. When you open the scene, click the “WeightbasedRandom” object in the hierarchy view
2. With WeightbasedRandom selected, press the “Play” button to run the project.
3. Notice how the “WB Rnd Scrip” component on the WeightbasedRandom object has generated a list of numbers in the “Utility Values” array. These can be tweaked to change the outcome. The higher a utility value is relative to the other utility values, the higher the chance it will be chosen.
4. With the game view selected, press the spacebar. The taller a block becomes, the more often it was chosen. From left-to-right, each block represents one of the elements in the Utility Values list.

You can increase and decrease the value of “Number of Runs,” shown right under the utility values list in the inspector, on the WeightbasedRandom. This indicates how many times the algorithm runs (eg. how many times you rolled the loot table or asked the Sim to decide what it wanted to do). Just be aware that I have not built the system to ignore zero-value options, but I felt that adding such complexities would dilute what I am trying to convey. If anyone wants this functionality added however, feel free to ask and I’ll look into it.

Enjoy responsibly and remember; gambling is not for kids!

The code:

Eh I’m working on it. I will update with code explanations of the prototype tomorrow. Until then, all of the functions in the prototype have in-depth comments on them.

This prototype only houses a single script, which illustrates how easy it is to write such a mechanism, letting it dynamically handle external input. In this case, the input is defined by how many child objects are attached to the object housing this script:

1. WBRndScript: This script handles all of the logic in the prototype.

1. WBRndScript:

1.0 Fields:

List<GameObject> cubes

This list houses references to all of the child objects used to generate utility values. They are added to a list, as that makes it possible to identify them via indexing.

Public List<float> utilityValues

The list of utility values. This list is generated dynamically, depending on the number of children that are underneath the current object.

List<float> probabilityValues

The list of calculated probability values. This list is generated dynamically, as each of the utility values are being processed.

 List<int> behaviourTracker

This list is used to keep track of the results of each run. It is generated dynamically, depending on the number of utility values that exist. At the end, these values are used to scale the size of the cubes, to visually illustrate the results.

Public int numberOfRuns

This int indicates how many times the algorithm should run each button-press. The value chosen here, dictates the sum of all of the values that can be stored in the behaviourTracker list, as each run will increment just one of the entries in that list.

1.1 void Awake():

Handles initialization. Additionally, the cubes list is initialized based on the number of children, whose length subsequently dictates the length of the utilityValues– and behaviourTracker lists.

1.2 void Update():

Listens to keypresses on the spacebar. When the spacebar is pressed, the algorithm will be run numberOfRuns times. The results are written in the console, then also used to scale each cube in accordance to how many times it was picked as the outcome. Each index of behaviourTracker is reset to zero right after scaling the cube, to ensure that it is ready to store the next round of runs.

1.3 void RunOnce():

This function is responsible for executing the algorithm, with each of the steps in the correct order:

1. Calculate the probability values (call CalculateProbability())
2. Summarize all of the probability values (call SummarizeList(probabilityValues))
3. Pick a random number between zero and the above sum(call PickRandomNumber(probabilityTotal))
4. Subtract each probability value from this random number, until zero is reached (call PickIndex(probabilityTotal, randomNumber))
5. Call the behaviour associated with the index of the probability value which caused the zeroing out (call ChooseOutcome(indexChosen))

1.4 void CalculateProbability():

This function populates the probability list. This is done by first summarizing the utility values, then for each utility value, calculate the probability by the following (where i is the current index for each of the utility values):

• P[i] = U[i] / (The sum of all utility values – U[i])

1.5 int PickIndex(float _randomNumber):

This function takes a value _randomNumber, then gradually subtracts each of the values stored in probabilityValues, until one of these subtractions causes the result to be zero. The index of the value causing the zeroing out, will be then be returned (indicating that index as being the chosen outcome).

1.6 float SummarizeList(List<float> _list):

This function takes a list of floats and returns the sum of them all, by simply adding them together via a foreach statement.

1.7 float PickRandomNumber(float _maxVal):

This function returns a random number between zero and _maxVal.

1.8 ChooseOutcome(int _index):

This function increments the value of behaviourTracker and index _index by 1, to indicate that this behaviour has been chosen.